发布时间:2024-07-08 21:25:03 浏览:
对于无约束的优化问题,常见的问题从目标函数的形式中可以分为:凸且光滑、非凸但光滑、非凸非光滑。问题的求解和目标函数的息息相关,下面首先介绍一些常用的优化问题求解方法。
一般无约束优化问题的形式为:
对于最速下降法的思想很朴素,给定初值,通过迭代的方法求出最优值,迭代的方向为函数的梯度的负方向,形式为: 从形式中可以看到,这里要求函数的梯度存在,也就是需要函数
光滑,并且只有函数为凸函数时,才能保证函数能收敛于全局最优解。
这里的难点在于得到最优的迭代步长 ,当步长取的太小会导致需要迭代的次数过多;当步长取的太大,可能会导致越过最优解,一直在震荡。
最速下降法的形式可以表示如下:
那最优的迭代步长
可以表示为:
。最优的迭代步长也变为求解一个优化问题,整个问题求解比较困难。
在工程上,我们使用被称为Armijo condition(sufficient decrease condition)的方法来近似的取的一个求解步长。其表达形式为:
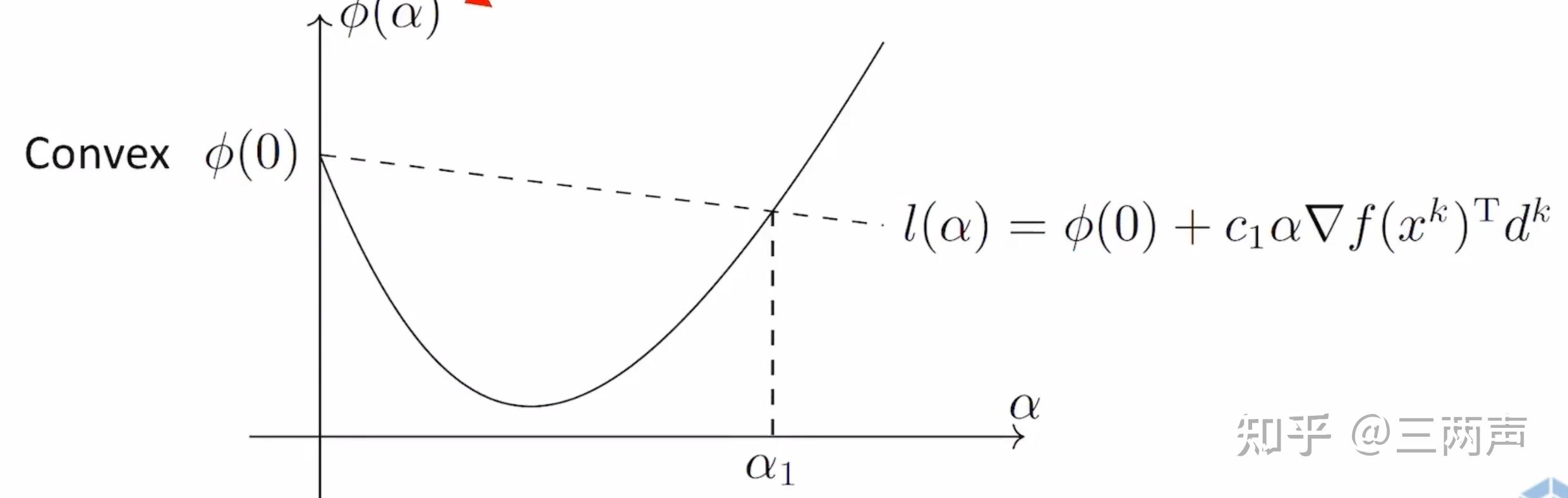
从几何意义上来看,Armijo condition是对梯度进行了缩放,然后选取虚线下方的一个步长来保证全局的下降性。
下面举例来进行说明:
针对10维的函数,可以给定任意初值,经过7650步的迭代,最优解收敛到精度以内。

为了更加直观化,将函数设置为2维,迭代的过程如下:
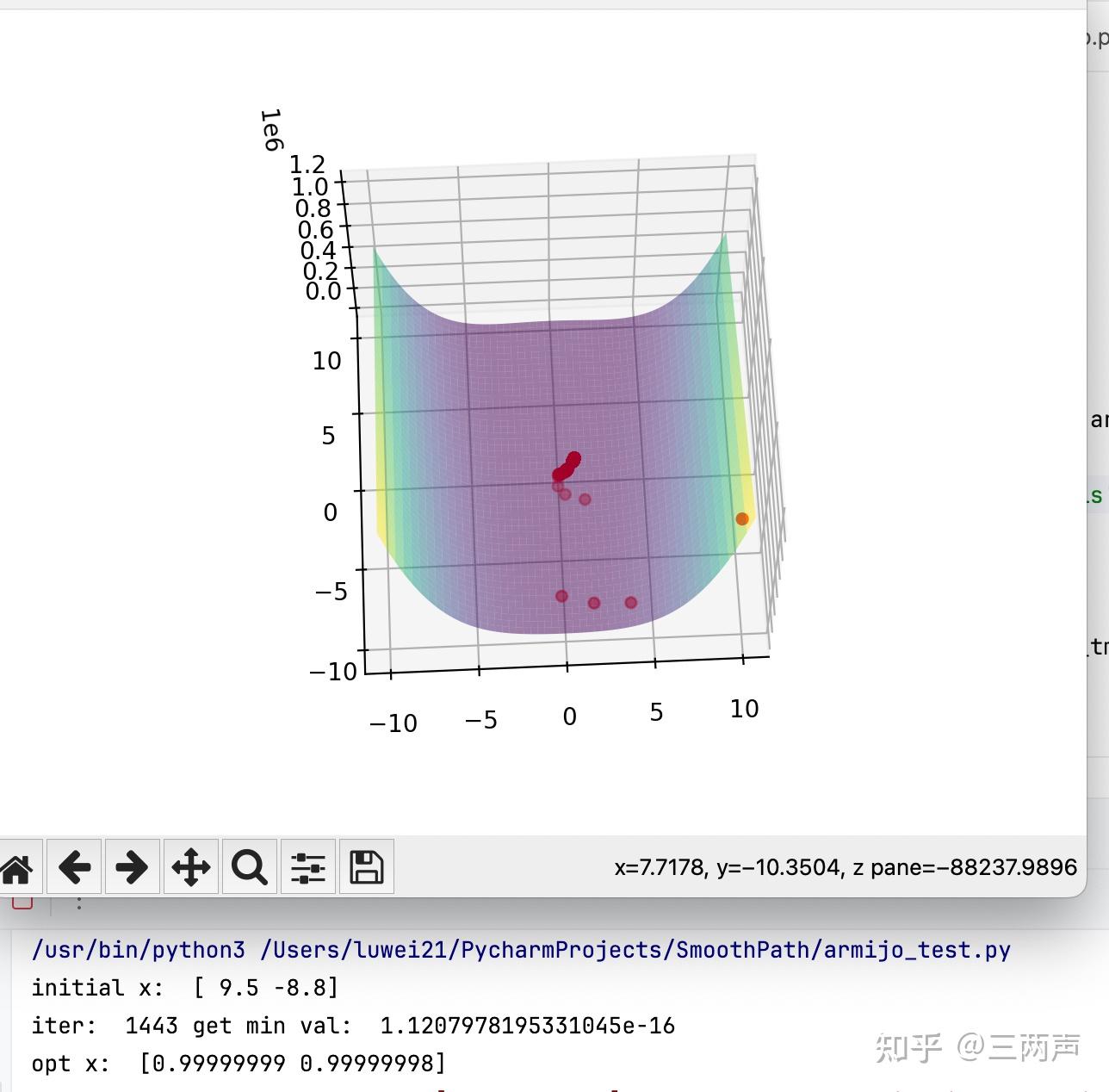
牛顿法的主要思想是利用函数的二阶信息,使得函数进行充分的下降。假设函数光滑且二阶导数处处存在,对函数进行二阶展开为:
二阶展开后,如果原函数的Hession矩阵正定即 ,函数的最小值存在为:
其中
称为牛顿步长。
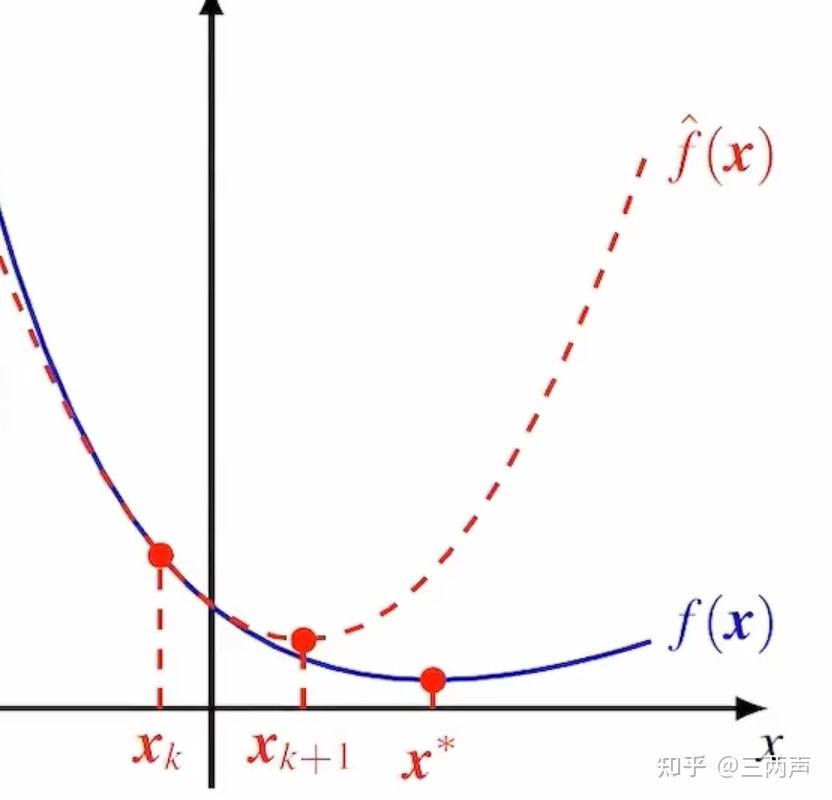
举例说明牛顿法,函数如下:
牛顿法只需要迭代6步就可以得到最优解
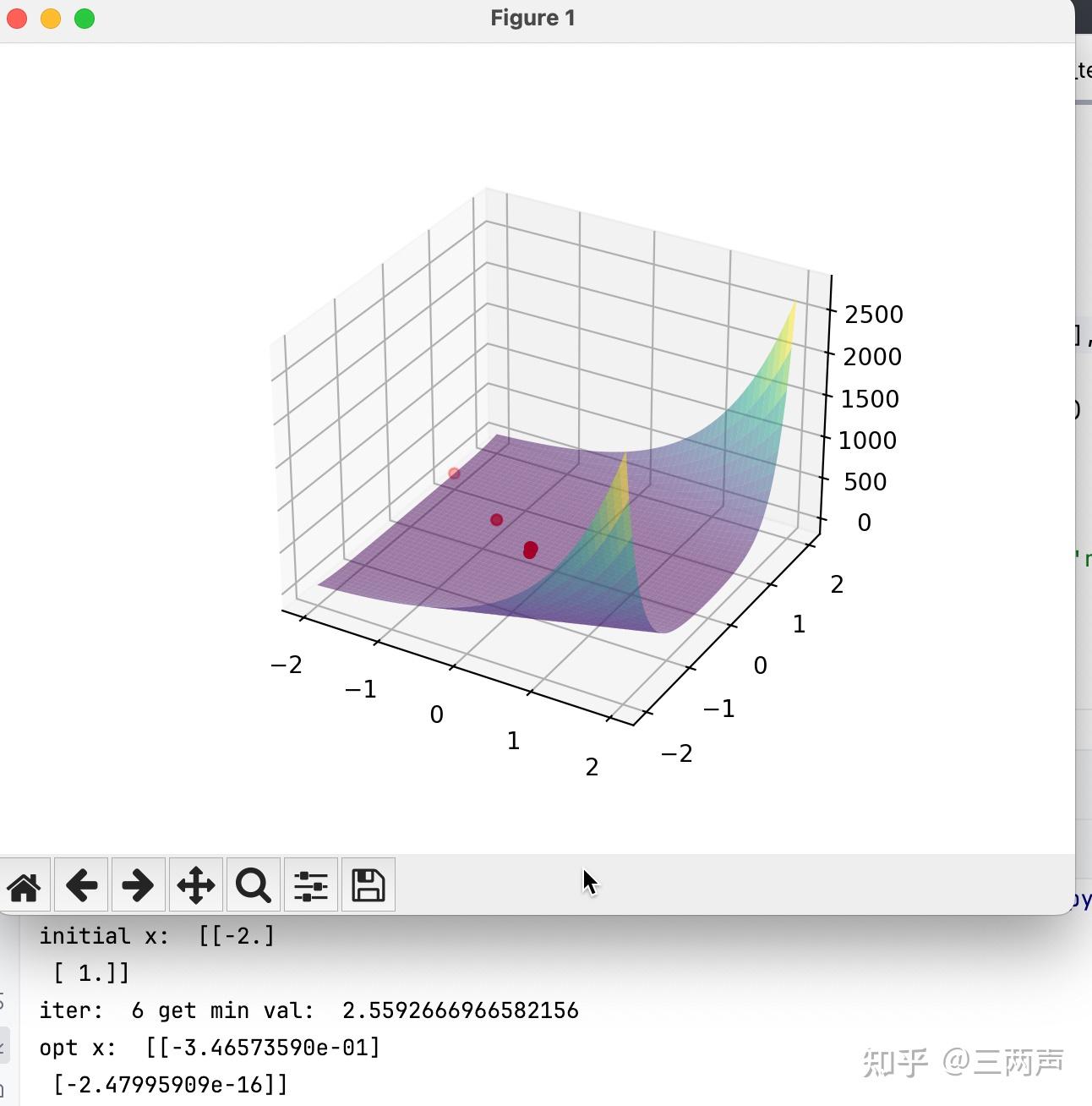
使用最速下降法,对相同的问题进行测试,可以看到求解的迭代次数明显增多。
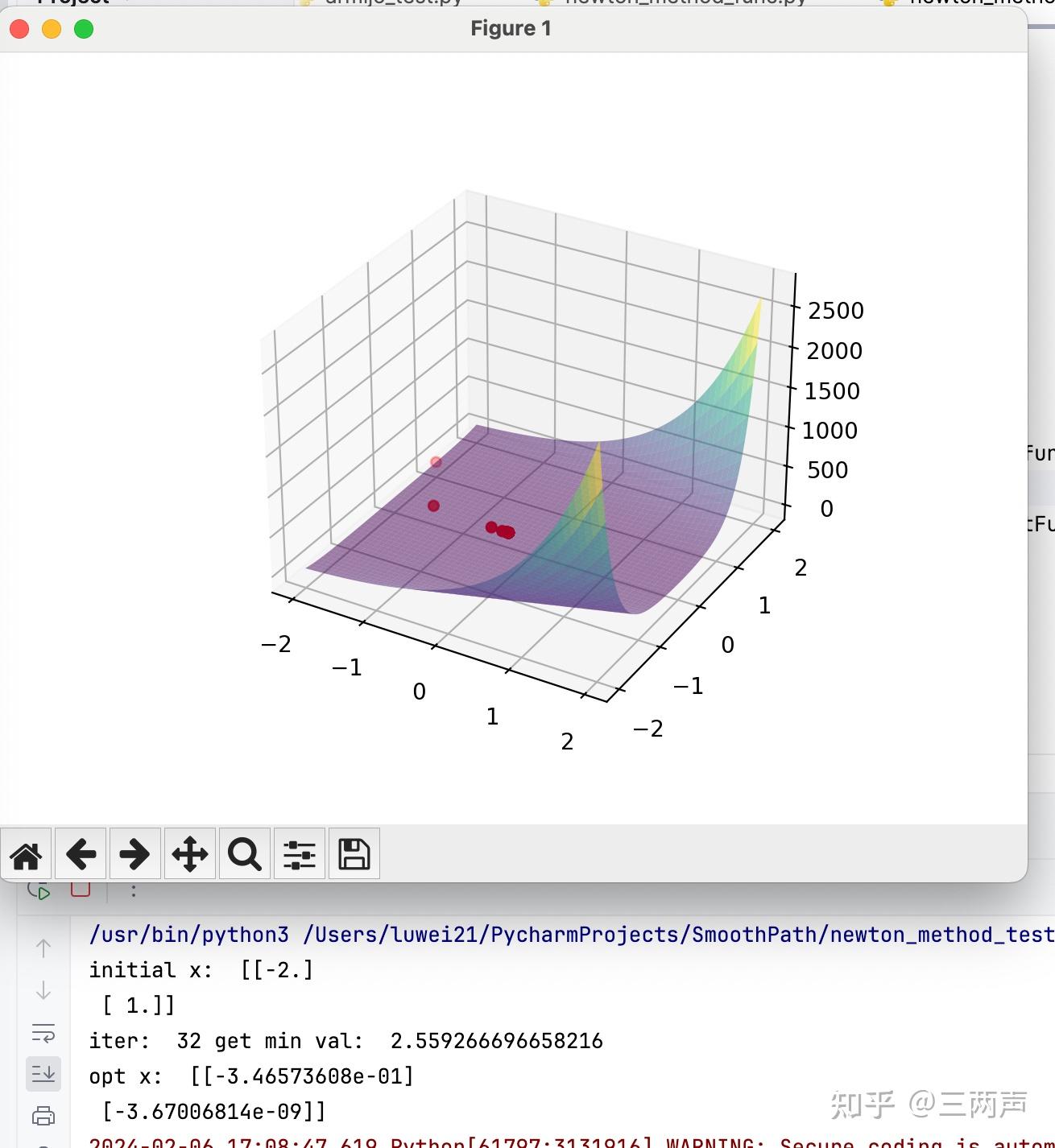
牛顿法需要函数的Hession矩阵严格正定,对于Hession矩阵奇异或者不定的情况,牛顿法不再适用。此时可以使用修正阻尼牛顿法进行求解,其求解的步骤如下

与牛顿法相比,使用严格正定的矩阵M,使得M矩阵足够接近于Hession矩阵。同时在线性搜索的步骤仍然可以使用Armijo condition来确定迭代的步长。
如果函数为凸函数,此时 ,
取 ,
如果函数非凸,此时Hession不定
,此时B矩阵是对角块矩阵,将其中的负特征值更换为正特征值。
牛顿法的缺点在于当二阶条件失效时,牛顿方法会失效,同时Hession矩阵的计算是比较耗时的,当问题非凸时,会得到一个无效的步长。
对于Hession矩阵严格正定的情况,求迭代的方向相当于求解如下问题:
拟牛顿法相当于求如下的问题:
为了保证第
步的方向
一定能使得函数值下降,则
与
的方向一定要是锐角才可以,则
其中 表明矩阵
一定是正定矩阵。
另外一个M矩阵的条件被称为正割条件,反映的是Hession矩阵中的曲率信息。此条件如下:
有了上述两个关于 基本条件,同时加上B矩阵归一化之后变动最小的目标函数,就可以得到大名鼎鼎的BFGS方法。
上述问题的解和
的具体形式无关,其结果为:
同时当 满足
时,
矩阵满足严格正定的条件,此条件其实表明,原函数为严格正定函数。
为了保证 的条件在原函数为一般函数时也成立,通过增加线性搜索条件来满足,此条件被称为
同时分为
版本。
weak Wolfe conditions:
strong Wolfe conditions:
在工程中weak版本的条件和strong版本的条件,迭代的次数相差的不多。
在非凸的函数中,BFGS方法其实不能保证梯度一定收敛到0的地方,此时需要加上cautions update(Li and Fukushima)条件来保证BFGS方法也适用于非凸的函数求解。
因此上针对严格凸与非严格凸的函数,BFGS方法的求解步骤如下:
严格凸的函数,求解步骤如下:

非严格凸的函数,为了保证收敛性,求解的步骤如下:

举例说明:
首先使用牛顿法求解:
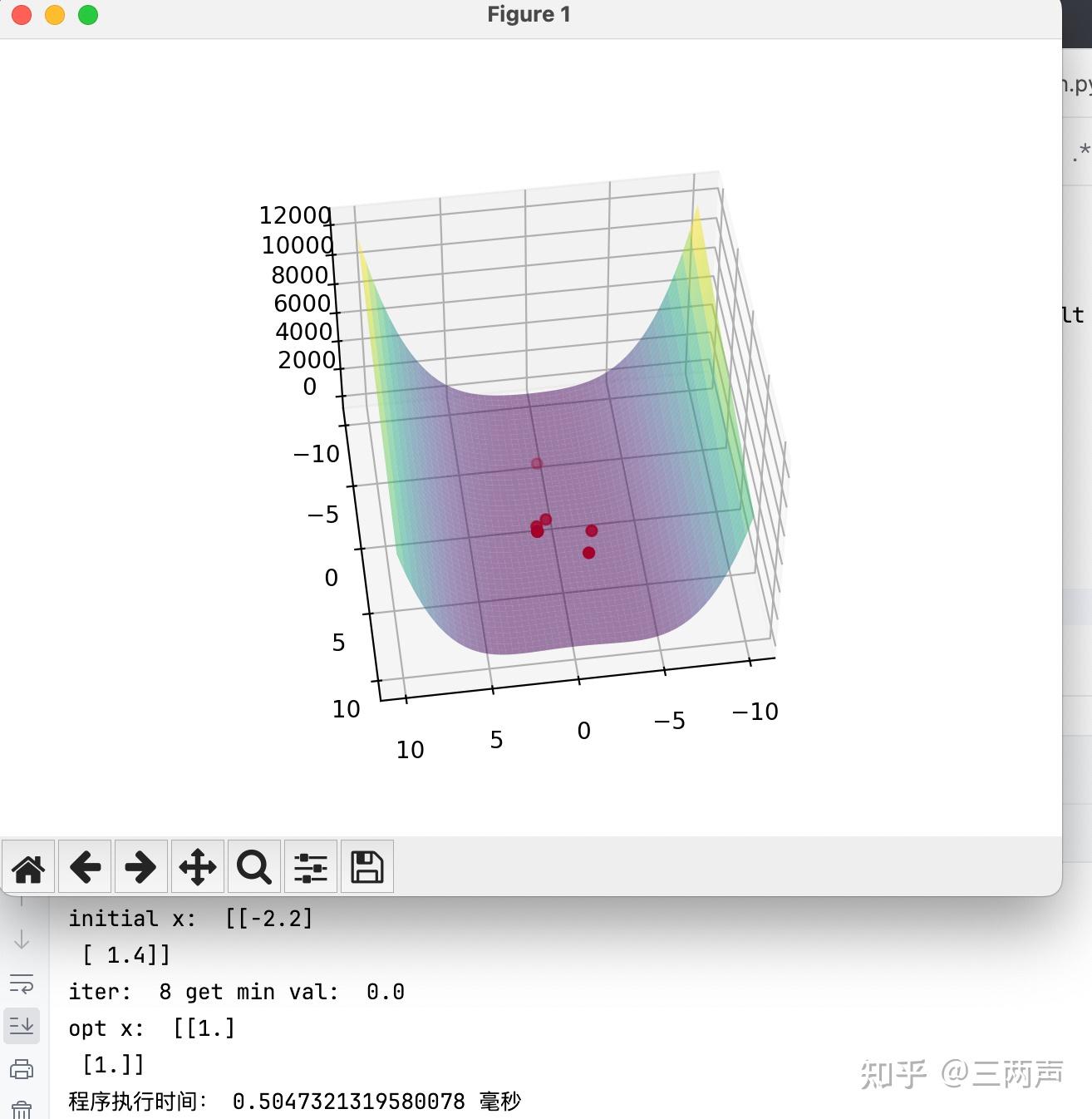
使用拟牛顿法进行求解:
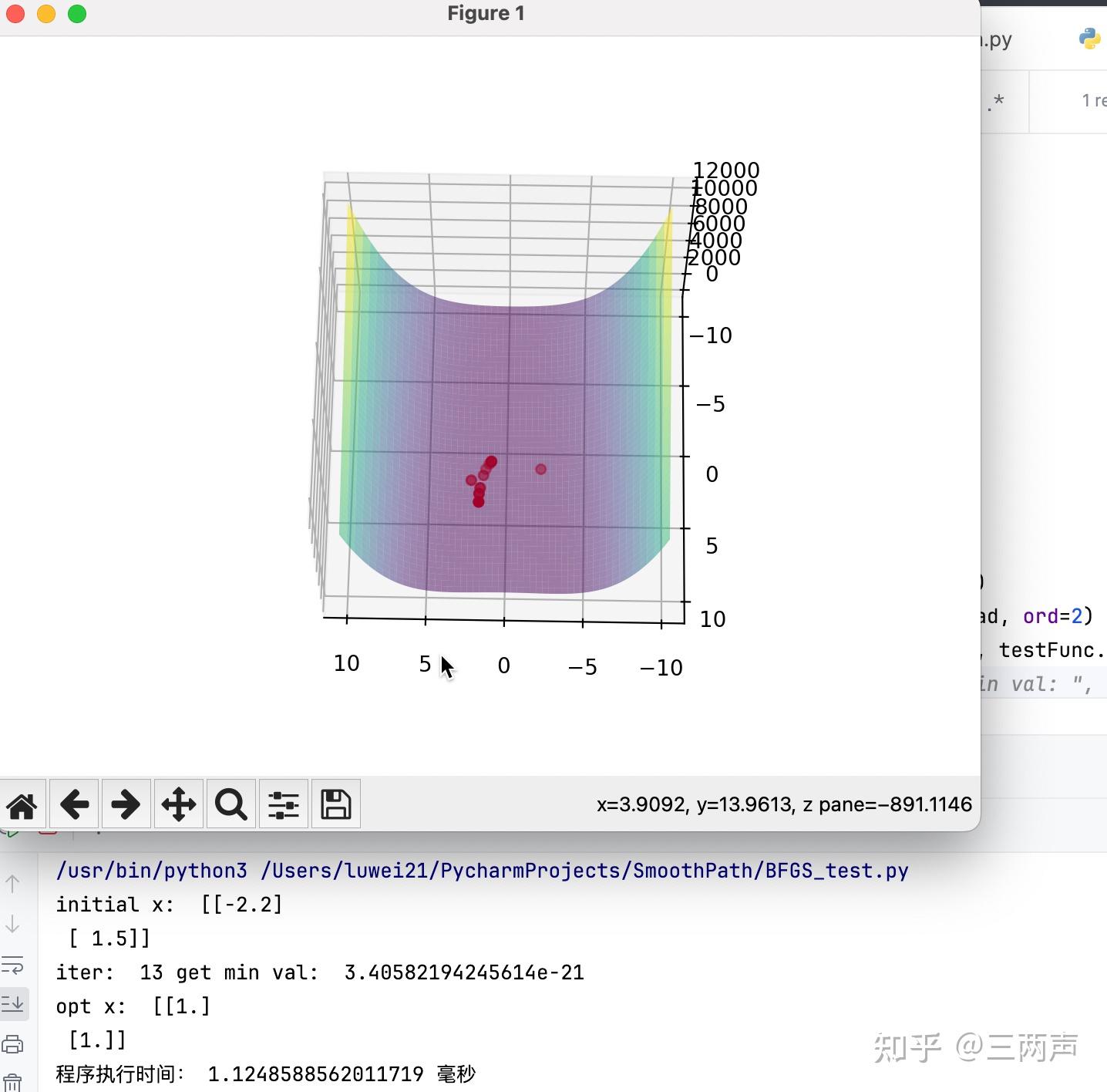
因为例子比较简单,从例子中可以看出,BFGS的求解时间并没有占据优势,但是当变量的数量增加时,BFGS的求解时间会优于牛顿法。同时BFGS加上Weak Wolfe Conditons具有更广的使用范围,对函数的凸和非凸没有要求,同时也不要求Hession矩阵一定存在,仅仅要求函数光滑,也就是函数的一阶导数存在。
L-BFGS的与BFGS相比,最主要的思想是整个迭代过程中,历史所有的 不是都有必要的。通过设置一个窗口,将超过窗口的
丢弃,通过设置窗口,可以降低矩阵
的秩,使得矩阵存储复杂度降低。
我们不直接存储 ,而是至多存储m对的
来还原当前点的曲率信息。在每轮的迭代中:
但是此时的计算复杂度为 ,可以通过如下的算法将复杂度降低为
:
举例说明,使用BFGS的例子进行说明,首先使用BFGS进行求解:
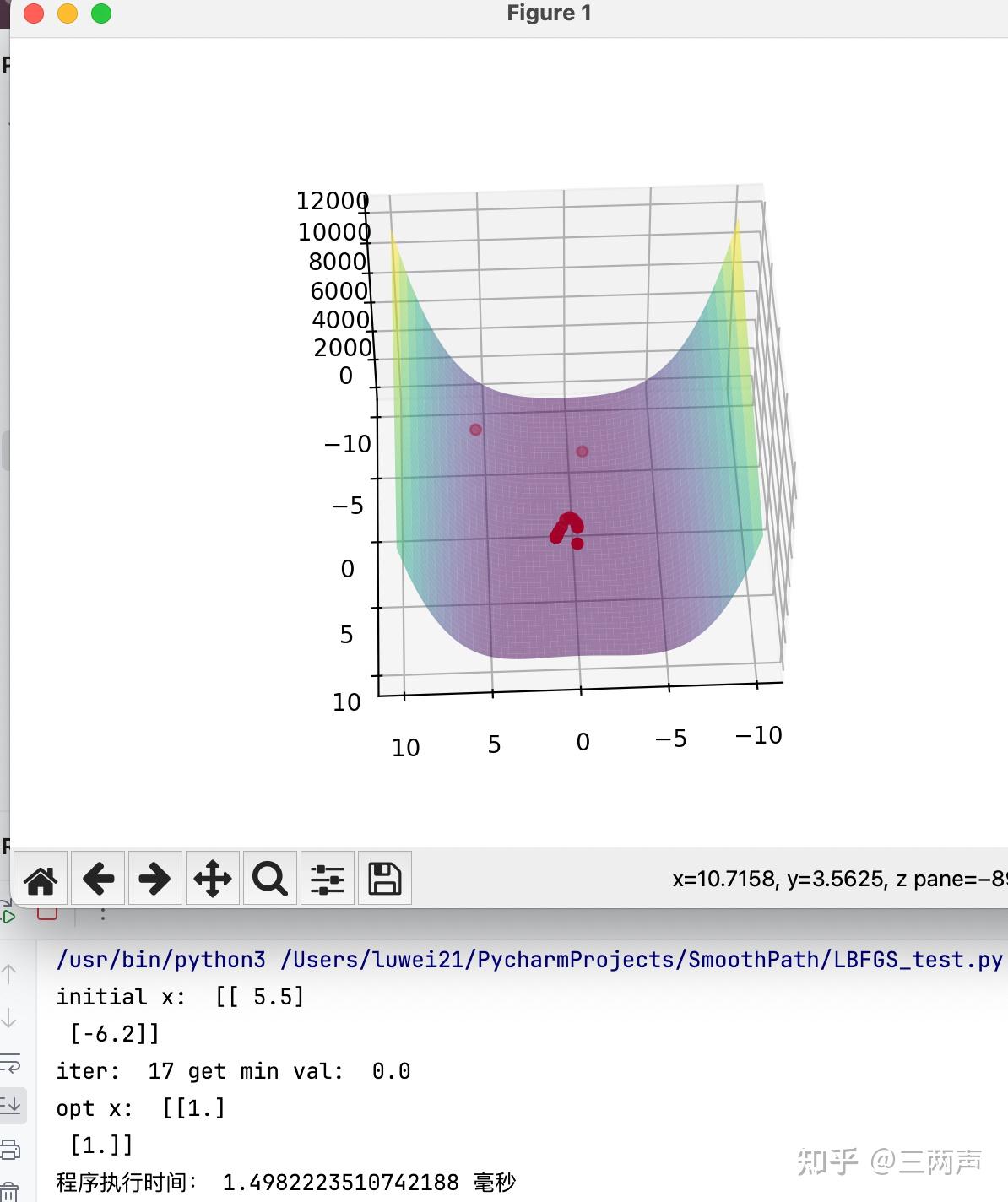
使用LBFGS进行求解:
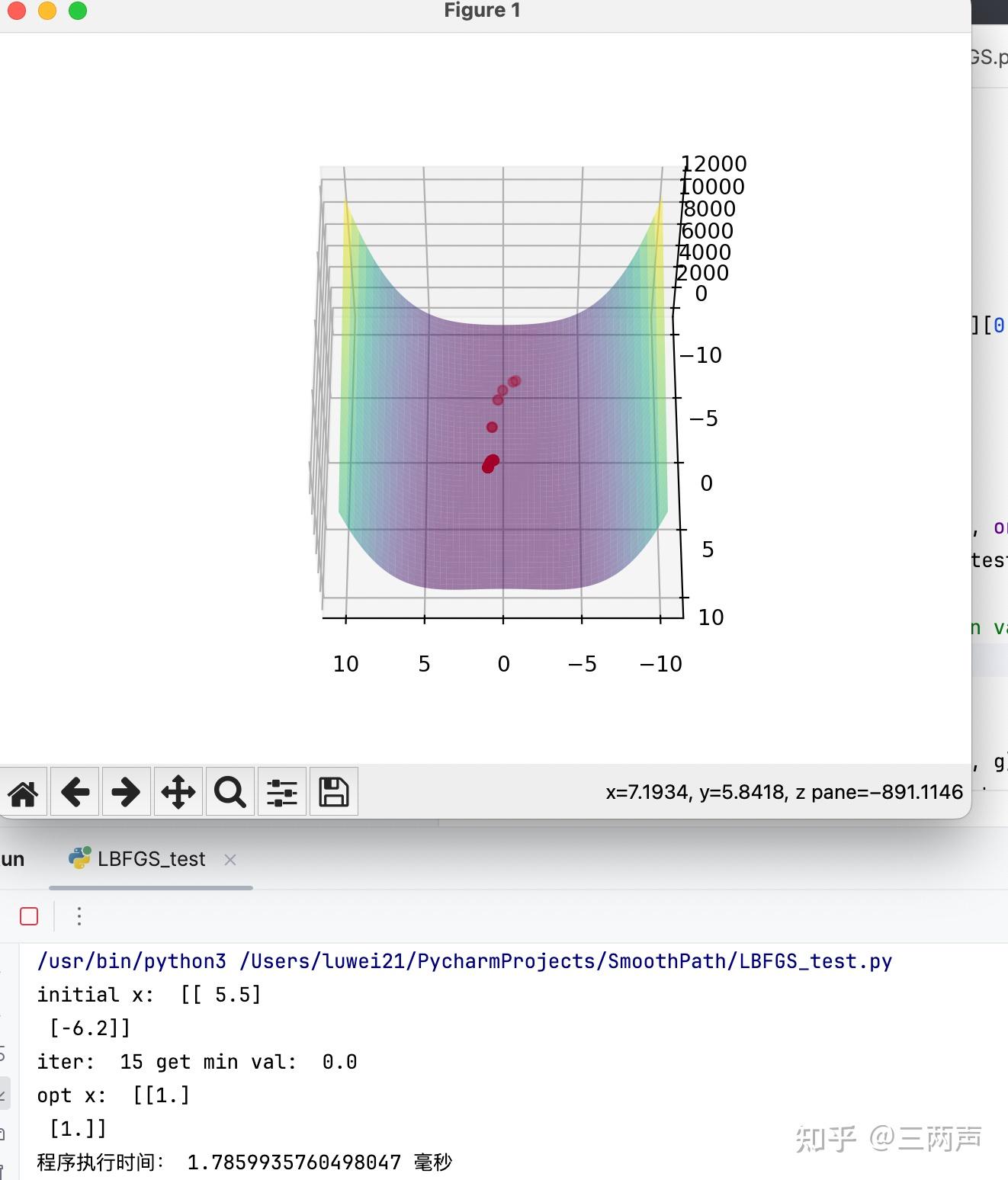
求解此问题时,LBFGS的迭代次数和求解时间还要由于BFGS方法。
在实践的过程中发现,有两一点需要特别注意
- L-BFGS初值的处理,L-BFGS初次迭代时,需要使用梯度进行迭代一步。
当函数非凸非平滑时,此时weak Wolfe conditions不再适用,针对此类问题,线性搜索的条件需要更换为Lewis & Overton line search,此条件的具体步骤如下:
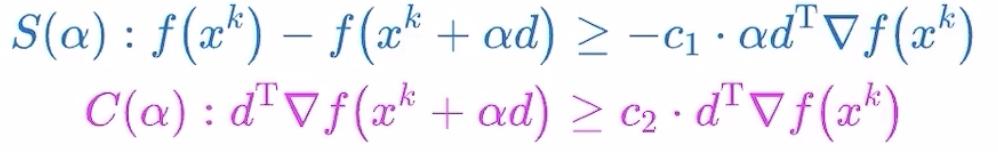
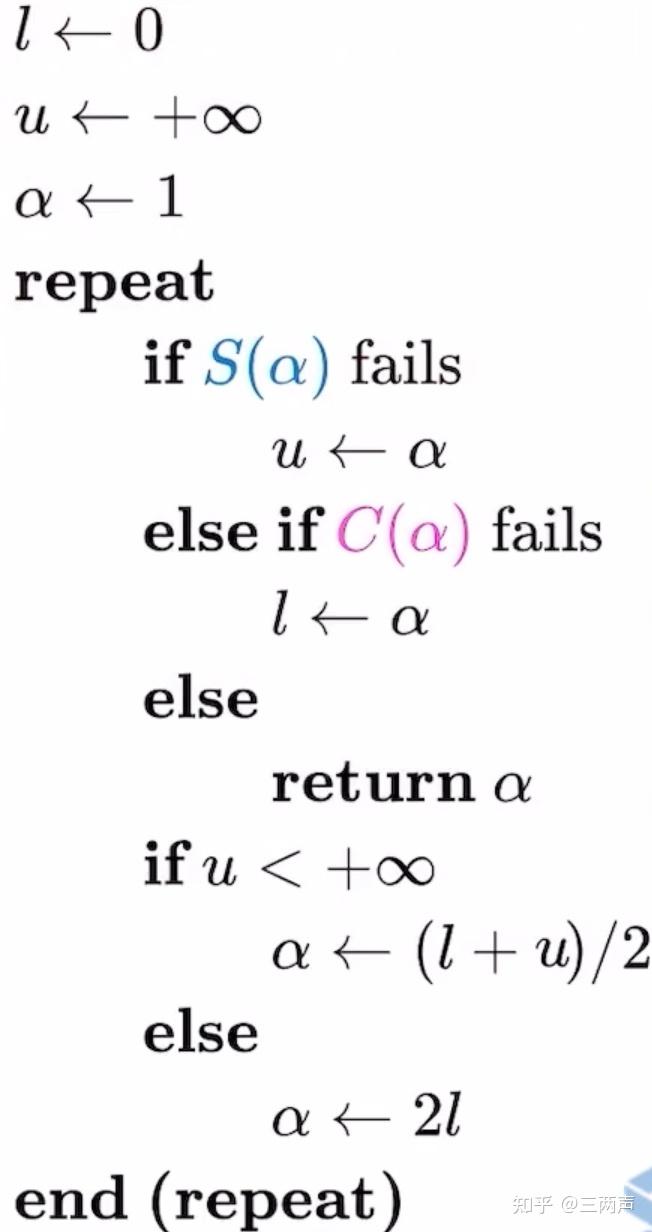
同样的进行举例说明,使用如下的函数: 将BFGS的线性搜索条件条件更换为Lewis & Overton line search,进行求解
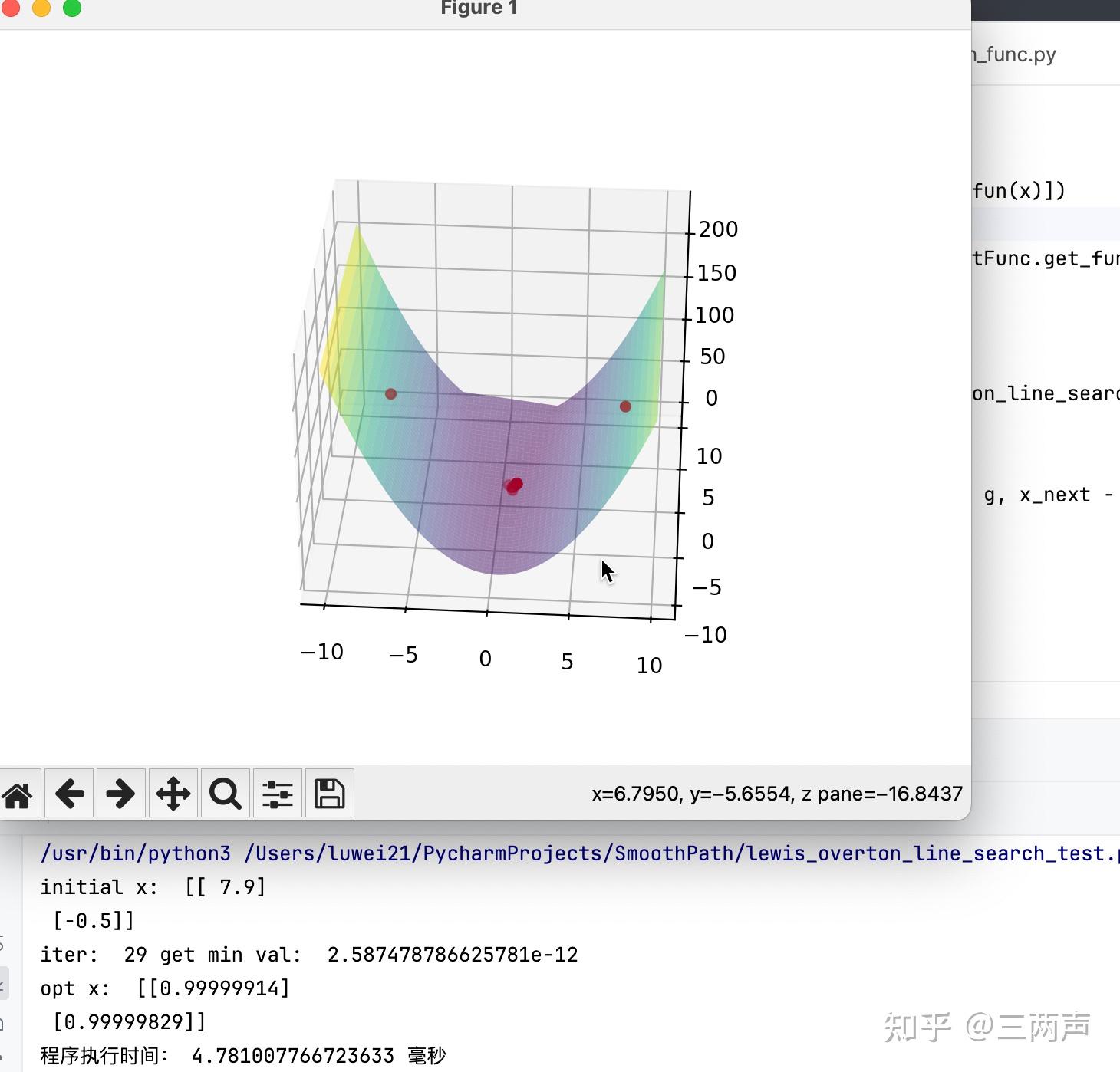
将L-BFGS的线性搜索条件条件更换为Lewis & Overton line search,进行求解
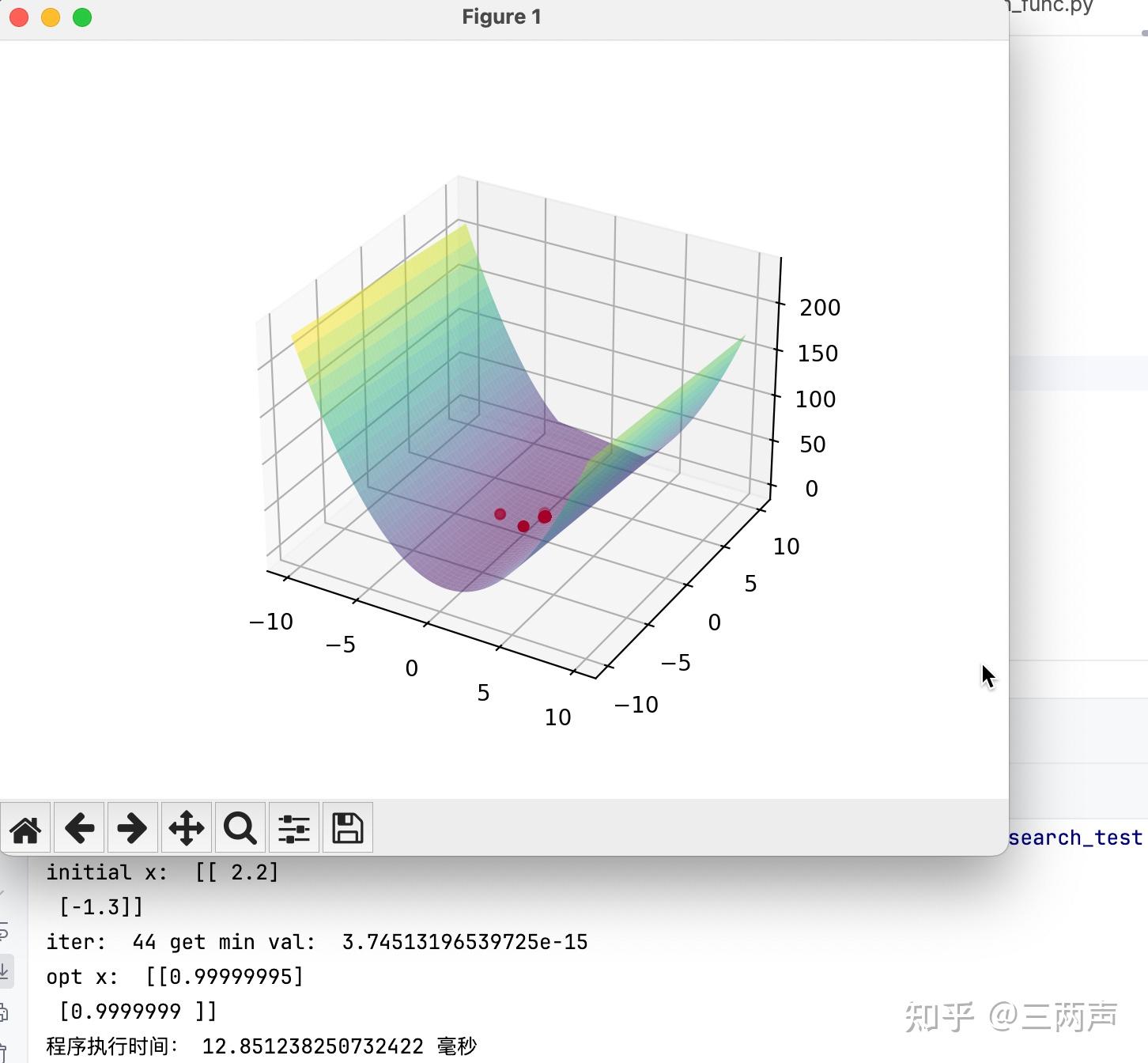
针对此例子,在相同的求解精度下,BFGS的求解效率要优于L-BFGS。
需要注意的是,非平滑的函数最优解有可能落在函数的不可导的地方,此时梯度的判断会失效,可以根据前后函数的变化值来进行判断。
CG方法是用来解决 的问题。解决
的问题,等价于解决
问题。
一般的步骤是:
- 给定n个互相共轭的的向量
,作为搜索的方向
计算步长与下一个 如何获取n互相关于
矩阵共轭的向量,有比较成熟的算法,被称为Gram-Schmidt process.同时对
的合适选择,简化整个过程的计算。
选取 ,此时共轭的向量
完成的求解的过程如下:

Newton-CG Method是将CG方法应用到 求解出来
.针对
可能非正定的情况,通过
来进行近似的求解。
完整的Newton-CG Method求解过程如下:

举例进行说明:
使用L-BFGS进行求解的结果如下:
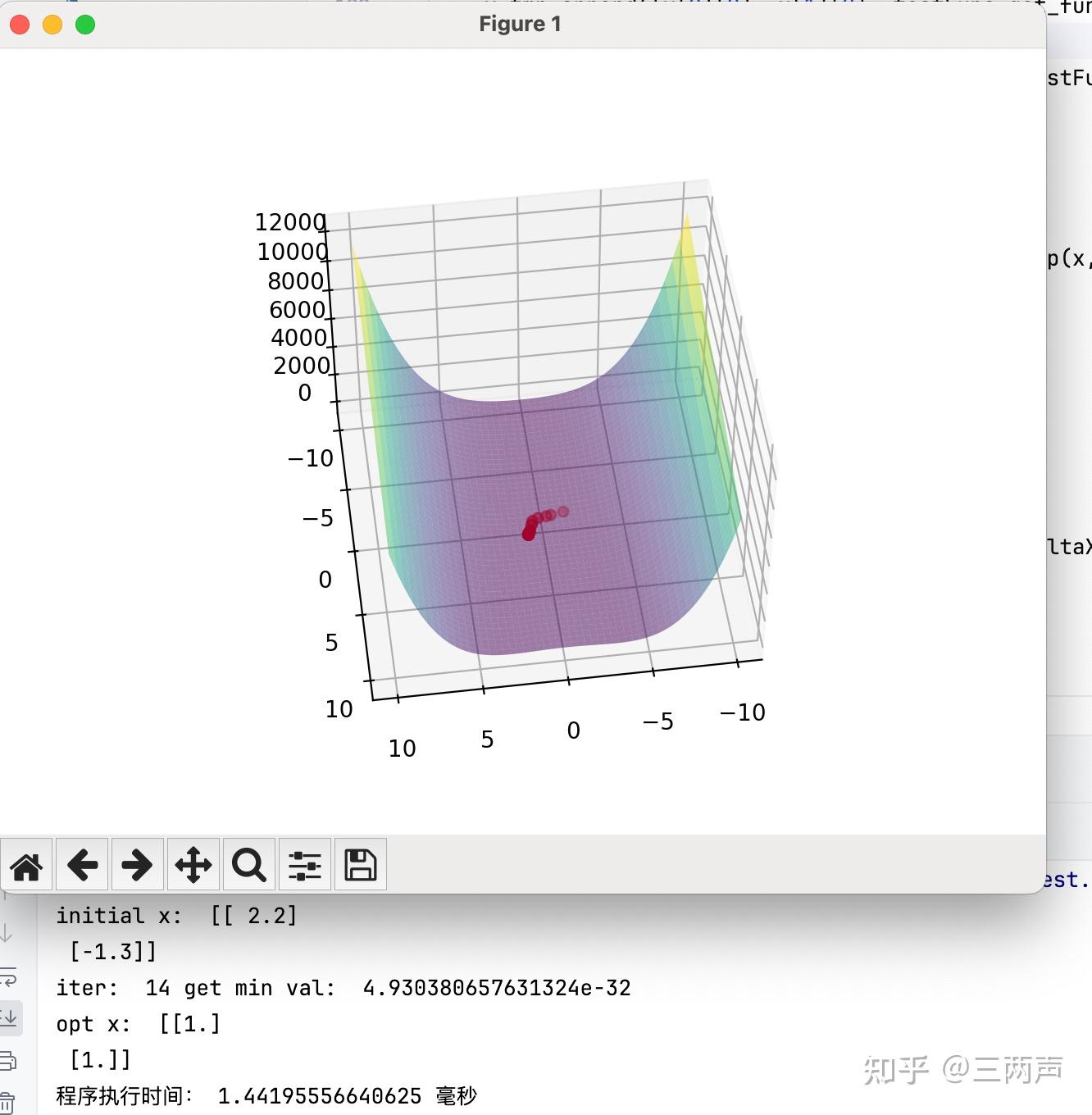
使用Newton-CG Method进行求解,求解的结果如下:
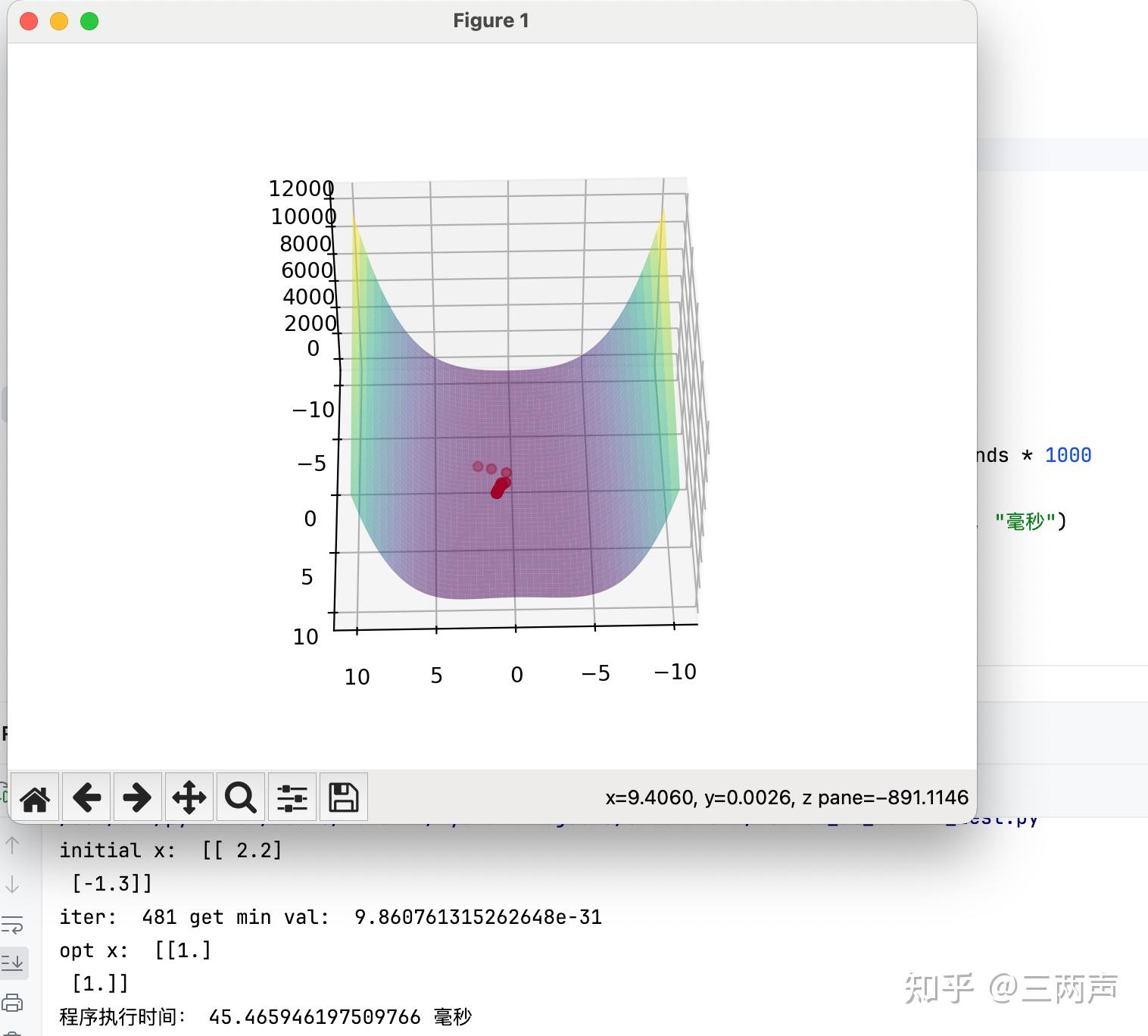
针对此例子,求解的速度上Newton-CG Method稍逊色于L-BFGS
前面介绍的所有求解方法的求解速度和花费的代价如下:
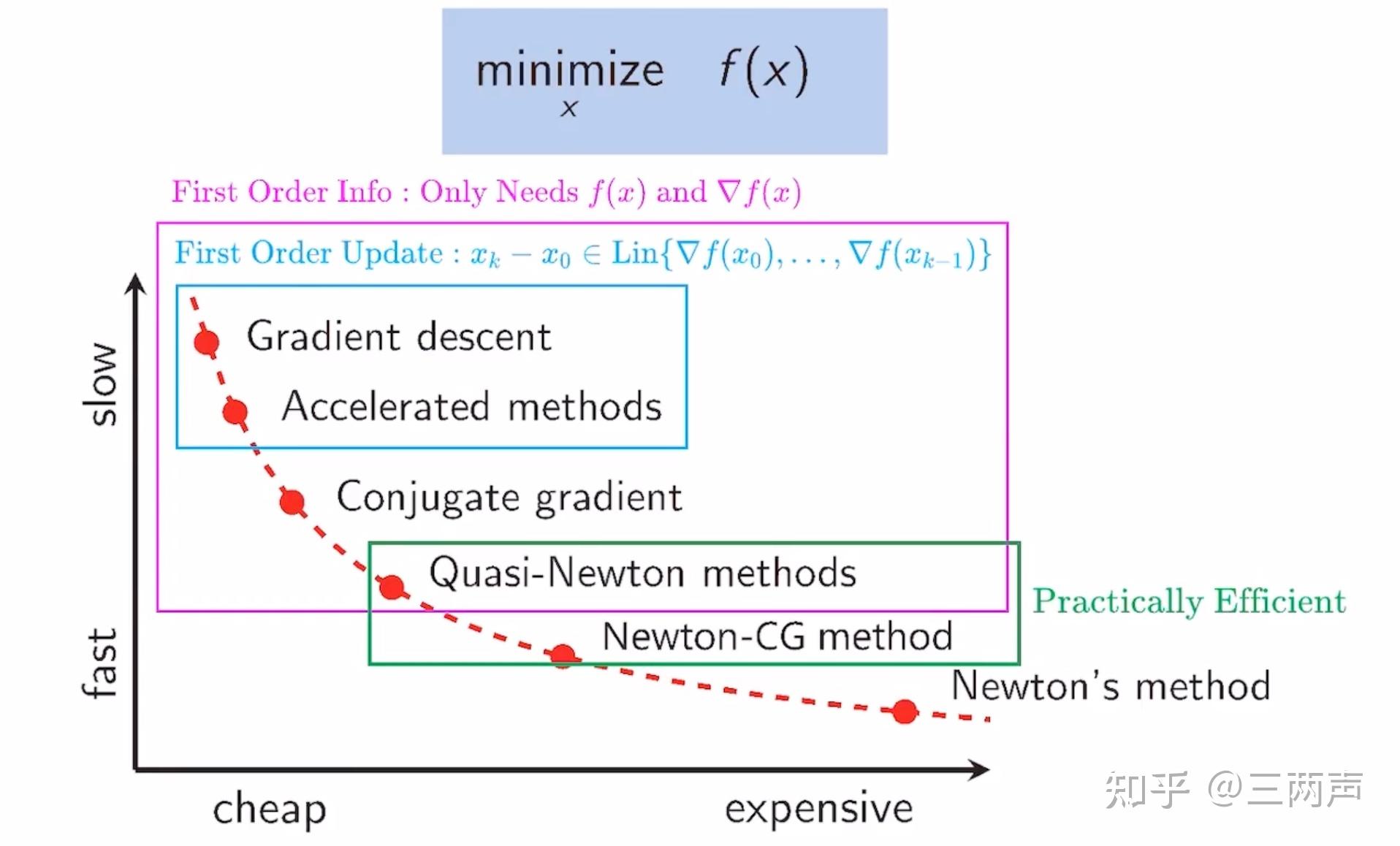
因为所举的自己维数比较低也比较简单,因此在求解速度不能一一匹配上。所有的求解例程均使用python在进行了测试,地址为:GitHub - lwtechnology/SmoothPath.
欢迎大家一起交流
































